「資産1000万を超えた人は複利の効果を感じるようになる！」←これ、実は間違ってます。
「え？嘘なの？」と思った方も多いでしょう。私も最初は「資産1000万を超えれば複利を実感できる！」とそう信じて節約や投資を続けていました。
でも、実際に資産1000万を超えて分かったのは、資産1000万で複利を実感できる人とできない人へ両極端に分かれてしまうということです。
実感できな人は資産5000万や資産1億を達成しても複利を実感できない可能性があります。
そこで、今回は「資産1000万を超えると複利の効果を感じるようになる！」のどこが間違っているのか、そして実際に資産1000万達成した身から複利効果の現実について赤裸々にお話しします。
最後まで見ていただければ複利に対する誤解が解けて、より現実的な投資戦略を立てられるようになるので、ぜひ最後まで見てください。
YouTubeでは動画バージョンも公開しています↓
そもそも複利とは何か
まず、複利について簡単におさらいしましょう。
複利とは、元本に利息が加わり、その合計額に対してさらに利息が付く仕組みです。
つまり「利息が利息を生む」状態のことです。
例えば、100万円を年利5%で運用した場合：
- 1年目：100万円 × 1.05 = 105万円
- 2年目：105万円 × 1.05 = 110.25万円
- 3年目：110.25万円 × 1.05 = 115.76万円
このように、元本だけでなく利息部分にも利息が付くため、時間が経つほど雪だるま式に増えていくのが複利の特徴です。
アインシュタインが「複利は人類最大の発明」と言ったとされるほど、長期投資において重要な概念の１つです。
なぜ「資産1000万で複利を感じる」と言われるのか
では、なぜ「資産1000万で複利を感じる」と言われているのでしょうか？
これは主に、よく使われている投資のシミュレーションが原因です。
多くのシミュレーションでは、毎年一定の年利（例えば年利5%）で計算されています。
例として1000万円を年利5%で運用した場合：
- 1年目の利益：50万円
- 2年目の利益：52.5万円
- 3年目の利益：55.1万円
確かに毎年の利益が50万円を超えてくると「お、複利効果が出てきた！」と感じやすくなります。
月割りでも4万円以上の利益が出るので、金額的にも実感しやすいはずですよね。
しかし、資産1000万を達成した人たちの多くがこう言うでしょう。「資産1000万では複利を感じないよ～感じる複利は夏の暑さと電気代の高騰だけさ」とね。
「え？じゃあ、資産1000万では複利が発生しないの？」と思われるかもしれませんが、実は複利自体はしっかり発生しています。
資産1000万でも複利の効果は大きいが、実感が難しい
では、実際に資産1000万を超えた私が何を感じたのか、正直にお話しします。
複利は確実に発動している
まず誤解を生まないために先に言っておきますが、資産1000万でも複利効果自体は間違いなく発動していますし、複利を実感できている人もいます。
投資元本が大きくなれば、同じ利回りでも得られる利益の絶対額は大きくなっていくからです。
例えば、私のポートフォリオが月間で2%上昇した場合：
- 資産500万円なら：10万円の利益
- 資産1000万円なら：20万円の利益
この差は確実に感じられますが、「雪だるま式に増える実感」を得られない人は多いのではないでしょうか？
ここが重要なポイントで、理論上は複利効果が働いているはずなのになぜか「雪だるま式に増えている」という実感は得られにくいんですよね。
なぜかと言うと年利1%あたりの変動額を見ていないからです。
年利が一定ではない現実
シミュレーションでは年利5%で一定ですが、実際の投資では：
- ある月は+8%
- 翌月は-5%
- その翌月は+3%
このように毎月や毎年の成績がバラバラであり、複利で雪だるま式に増えることを実感しにくくなっています。
もし仮にS&P500へ1999年に1000万円を一括投資し、9年間そのまま放置した場合は下画像のグラフになります。
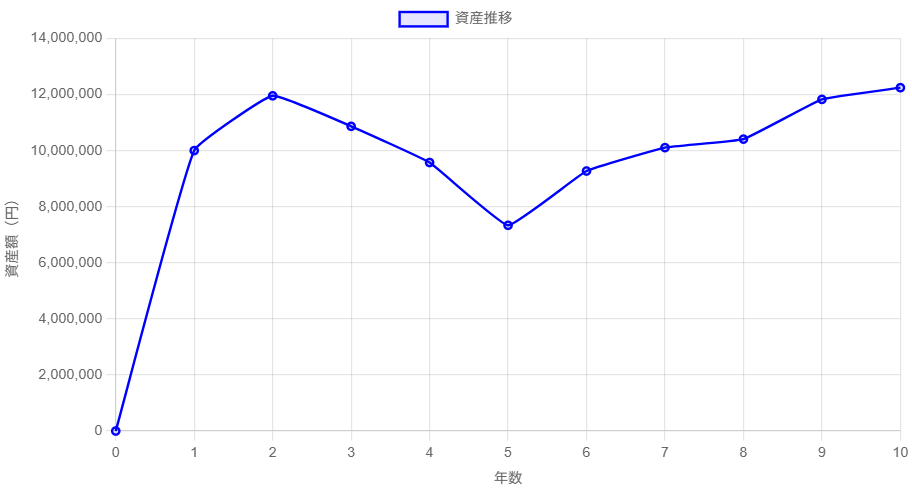
少しグラフが分かりにくいかもしれませんが、1999年を年数1としており、そのタイミングで1000万円を一括投資しています。
正直、このグラフでは上下に金額が動いているので複利が発生していることを実感しにくいですよね。
特に大きく下がっているところを見ると本当に複利が発生しているのか？と疑いたくなると思います。
でも、実は資産が下がっている場面でも複利は発生しているので、そちらについては次の章で解説します。
もう少し分かりやすく複利を理解するために過去データの運用資産と1999年～2007年までの単純平均年利3.47%で運用した表を用意しました。
| 年 | 過去データ 年利 | 過去データ 運用資産額 | 前年比増減額 (過去データ) | 単純平均年利（3.47%） 運用資産額 | 前年比増減額 (単純平均年利) |
|---|---|---|---|---|---|
| 1999 | 19.53% | ¥11,953,000 | ¥1,953,000 | ¥10,347,000 | ¥347,000 |
| 2000 | -9.10% | ¥10,865,137 | -¥1,087,863 | ¥10,705,749 | ¥358,749 |
| 2001 | -11.89% | ¥9,573,165 | -¥1,291,972 | ¥11,076,827 | ¥371,078 |
| 2002 | -23.37% | ¥7,338,981 | -¥2,234,184 | ¥11,461,269 | ¥384,442 |
| 2003 | 26.38% | ¥9,274,383 | ¥1,935,402 | ¥11,859,258 | ¥397,989 |
| 2004 | 8.99% | ¥10,108,127 | ¥833,744 | ¥12,271,061 | ¥411,803 |
| 2005 | 3.00% | ¥10,411,371 | ¥303,244 | ¥12,697,008 | ¥425,947 |
| 2006 | 13.62% | ¥11,829,195 | ¥1,417,824 | ¥13,137,390 | ¥440,382 |
| 2007 | 3.53% | ¥12,246,678 | ¥417,483 | ¥13,592,492 | ¥455,102 |
シンプルに年平均リターンが3.47%で固定されてれば年々リターンが増えていくので、上表のように複利によって前年比増減額が順調に増えていき、雪だるま式に資産が増えることを実感しやすいです。
一方で、過去データでは大きく資産が増える年もあれば大きく減る年もあり、前年比増減額を見ても複利が発生しているのか正直分からないですよね。
例えば2003年から2007年までは毎年プラスなので複利が発生しているはずですが、前年比増減額を見ても複利を実感できないと思います。
むしろ複利で増えたというよりも単純にその年の株式市場の盛り上がりによって資産が増減した結果、最終的には増えてたという風に見えますよね。
これこそが資産1000万では複利を実感できない正体でもあります。
でも、実は過去データの場合でも年利1%あたりで動いた金額を見れば複利が仕組みとして働いてることを実感できます。
年利1%あたりで動いた金額を見れば複利が分かる
S&P500の過去データで求めた前年比増減額をその年の年利で割ると「年利1%あたりの変動額」を計算できます。実際の結果が下表です。
| 年 | 過去データ 年利 | 過去データ 運用資産額 | 前年比増減額 (過去データ) | 年利1%あたり の変動額 |
|---|---|---|---|---|
| 1999 | 19.53% | ¥11,953,000 | ¥1,953,000 | 100,000円 |
| 2000 | -9.10% | ¥10,865,137 | -¥1,087,863 | 119,545円 |
| 2001 | -11.89% | ¥9,573,165 | -¥1,291,972 | 108,660円 |
| 2002 | -23.37% | ¥7,338,981 | -¥2,234,184 | 95,600円 |
| 2003 | 26.38% | ¥9,274,383 | ¥1,935,402 | 73,366円 |
| 2004 | 8.99% | ¥10,108,127 | ¥833,744 | 92,741円 |
| 2005 | 3.00% | ¥10,411,371 | ¥303,244 | 101,081円 |
| 2006 | 13.62% | ¥11,829,195 | ¥1,417,824 | 104,099円 |
| 2007 | 3.53% | ¥12,246,678 | ¥417,483 | 118,267円 |
ここで少しだけ補足させてください。『年利1%あたりの変動額』が示すのは、実はその年の『投資元本（期首の資産額）』そのものです。
例えば1000万円が元本なら、1%の変動は10万円ですよね？
つまり、この数字を見れば『あなたの投資の土台となる元本が、年々どれくらい大きくなっているのか』が直感的に金額でわかります。
今回はこの『1%あたりの動き』に注目して複利を実感できるように説明します。
まず一番最初に見てほしいのは2003年から2007年のデータです。
前年比増減額だけを見ていた時は年々増える金額が順調に上がっている訳ではないので、資産1000万クラスでも複利を実感しにくかったと思います。
一方で、年利1%あたりの変動額を見ると順調に増加しており、まるで雪だるまのようじゃないですか？
なぜ雪だるまのように上がっているかと言うと、前年に増加した資産分にも年利が上乗せされるからです。要は複利が働いているからですね。
特に2003年と2007年では1%あたりの変動額に4万円以上も差があるので複利を実感できます。
でも、単純な年利や前年比増減額だけを見ると2007年よりも2003年や2004年の方が複利で増えてるような勘違いを起こしそうですよね。
つまり、単純な年利や前年比だけを見ると資産1000万規模でも複利は分かりにくいですが、1%あたりの変動額を見れば複利の効果を実感できます。
ちなみに毎年固定の年利で見た場合でも年利1%あたりの変動額がしっかり大きくなっています。
| 年 | 単純平均年利（3.47%） 運用資産額 | 前年比増減額 (単純平均年利) | 年利1%あたり の変動額 |
|---|---|---|---|
| 1999 | ¥10,347,000 | ¥347,000 | 100,000円 |
| 2000 | ¥10,705,749 | ¥358,749 | 103,386円 |
| 2001 | ¥11,076,827 | ¥371,078 | 106,939円 |
| 2002 | ¥11,461,269 | ¥384,442 | 110,790円 |
| 2003 | ¥11,859,258 | ¥397,989 | 114,694円 |
| 2004 | ¥12,271,061 | ¥411,803 | 118,675円 |
| 2005 | ¥12,697,008 | ¥425,947 | 122,751円 |
| 2006 | ¥13,137,390 | ¥440,382 | 126,911円 |
| 2007 | ¥13,592,492 | ¥455,102 | 131,153円 |
というか、3.47%の固定年利であれば年利1%あたりの変動額を単純に全て3.47倍すれば前年比増減額になります。
これによって固定年利のシミュレーションであれば前年比増減額を見るだけでも複利を分かりやすく認識しやすくなっています。
おそらく、資産1000万を達成しても複利を実感できない方は固定年利のシミュレーションが前提にあるせいで、年利1%あたりの変動額の推移を意識していなかったのだと思います。
固定年利による複利ばかりイメージしていると資産5000万や1億になっても複利の実感が湧きにくいかもしれませんね。
私も資産1000万ありますが、この事実に気づくまでは複利の実感が湧きにくかったです。
これで資産1000万でも複利を実感できない原因と実際に複利が働いていることを説明できましたが、では資産が下落している時は複利がどうなっているのでしょうか？
資産下落時の複利について
実際に資産が下落している2000年～2002年だと年利のマイナス幅と前年比増減額が年々大きくなっており、「複利なんて考えてる場合じゃない！」と思ってしまうかもしれません。
しかし、ここでも注目してほしいのが、年利1%あたりの変動額の推移です。
| 年 | 過去データ 年利 | 過去データ 運用資産額 | 前年比増減額 (過去データ) | 年利1%あたり の変動額 |
|---|---|---|---|---|
| 1999 | 19.53% | ¥11,953,000 | ¥1,953,000 | 100,000円 |
| 2000 | -9.10% | ¥10,865,137 | -¥1,087,863 | 119,545円 |
| 2001 | -11.89% | ¥9,573,165 | -¥1,291,972 | 108,660円 |
| 2002 | -23.37% | ¥7,338,981 | -¥2,234,184 | 95,600円 |
| 2003 | 26.38% | ¥9,274,383 | ¥1,935,402 | 73,366円 |
| 2004 | 8.99% | ¥10,108,127 | ¥833,744 | 92,741円 |
| 2005 | 3.00% | ¥10,411,371 | ¥303,244 | 101,081円 |
| 2006 | 13.62% | ¥11,829,195 | ¥1,417,824 | 104,099円 |
| 2007 | 3.53% | ¥12,246,678 | ¥417,483 | 118,267円 |
資産が減少している2000年から2002年にかけて、「年利1%あたりの変動額」はどうなっているでしょうか？
2000年の約11万9千円、2001年の約10万8千円、そして2002年の約9万5千円と年々減少していますよね。
これは資産が増加する時に「年利1%あたりの変動額が増加していくこと」が増える複利なら、資産が減少する時に「年利1%あたりの変動額が減少していくこと」は減る複利とも言えます。
つまり、元本が減ってしまうと、たとえ同じマイナス10%の利回りでも、失う金額の絶対値は小さくなります。
例えば1000万円の10%減は100万円ですが、500万円の10%減は50万円です。失う金額だけ見ると小さく感じるかもしれません。
「え！じゃあ、資産が減少する時も複利が減少幅を小さくしてくれるんだ～！ラッキー！」と思うかもしれませんが、これは決して有利な状況ではありません。
なぜなら、減ってしまった元本を元の水準に戻すには、下落時よりもより大きなパーセンテージでの上昇が必要になるからです。
下落した資産を元に戻すために必要な上昇
もしあなたの資産が1000万円から50%減って500万円になったとします。
この500万円を元の1000万円に戻すには、100%の上昇が必要ですよね？
| 減少の割合 | 資産額 | 増加の割合 |
|---|---|---|
| 50%減少すると↓ | 1000万円 | |
| 50%減少すると↓ | 500万円 | 100%増加すると↑ |
| 250万円 | 100%増加すると↑ |
では、もしその500万円が、さらに50%減って250万円になってしまったらどうでしょう。
50%の減少で失う金額は小さくなりますが、この250万円を元の1000万円に戻すにはなんと300%（つまり4倍！）もの上昇が必要になります。
このように資産が下落する局面では元本が小さくなることで、その後の回復に必要な上昇率がどんどん大きくなってしまいます。
もちろん資産が下落すると1%あたりの変動額もだんだん小さくなってしまうので、増える複利を利用しても回復に大きなパワーが必要です。
これが「減る複利」、別名「逆複利」や「負の複利効果」の怖いところであり、資産形成において不利に働く要因と言えます。
資産1000万で複利を実感できるのは1%あたりの変動額に気づく人
というわけでまとめると、資産1000万で複利を多くの人が実感できないのは固定年利によるシミュレーションのイメージが原因であり、本当は資産1000万でも複利を十分に実感できます。
特に１％あたりの変動額を推移にすると分かりやすいので、ぜひ自身の資産で計算してみてください。
資産取り崩しシミュレーションを作りました！（下画像）
年利の標準偏差やインフレ率も無料で設定できるので、ぜひ活用してください。
